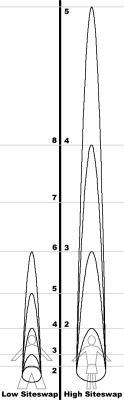
Siteswap : How does it work?

Siteswap is a notation used in juggling, and it can be applied to diabolo, based on the assumption that diabolo can be considered one handed juggling. When doing aerial diabolo (2, 3, more), the diabolos are thrown at an even pace, defining a rhythm where a diabolo is thrown on every beat. Siteswap links a number to the height of each throw. Writing a sequence of numbers is then writing a sequence of throws. When varying the height of throws, the order in which diabolos are caught can change, hence the name: site swap.

Theory

A number N matches the amount of time that the diabolo spends in the air before being re-thrown N beats later, or putting it another way the amount of time necessary for N-1 diabolos to be thrown before that diabolo is re-thrown.

For a throw of value 3, two throws can be done before that diabolo is caught and thrown again, no more. On the right is an illustration with the triangle notation for siteswap.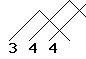

We therefore need two types of notation; N in high-notation matches the height needed for N high diabolos. N in low-notation matches the height needed for N low diabolos.
The relation between the two is: N high = (2N) 0 low.
For instance: 3 high = 60 low.

Getting practical Practically speaking, the number N is associated to the height at which one would juggle N diabolos. The drawing on the left is worth a thousand words and gives an idea of the height of each number. However, it doesn’t tell us what happens for numbers 0 and 1. - 0: The string is empty; there is no diabolo ready to be thrown. In a high carousel, this can be used to do a pirouette, string skip, etc… In a low carousel, there is not enough time for a pirouette (a 00 is necessary for this, which bestaucasinosonline.com/sa/ corresponds to the 0 in high-notation). - 1: The diabolo must be thrown again 1 beat later, without any other throw in between. In high-notation, this usually leaves time for fast tricks such as suns, suicides, magic knots, etc… In low notation, the 1 is too short for these kinds of tricks; it is simply a break in the rhythm. The 1 is an exception to the rule N high = (2N)0 low since in reality we 're more likely to have 1 high = 11 low (rather than 20 low).

Validity

For a sequence to be valid, 2 diabolos can not be caught at the same time. To check this, the difference between the values of 2 throws can’t be equal to the spacing between these throws. For instance, a sequence with includes 43 is not valid because 4-3=1, which is the spacing between 4 and 3 (1 beat).
The triangle notation can also be useful for tracking potential collisions:

The average rule

The average of the numbers in the sequence must be an integer which is the number of diabolos used:
(sum of the throws) / (length of the sequence) = number of diabolos
This can help validating a sequence:
- 441 might be valid since (4+4+1)/3 = 3 diabolos
- 535 is not valid since (5+3+5)/3 = 4.33 diabolos

Excited siteswaps

Some sequences are known as ‘excited’; the sequence is valid but it is impossible to start it from a regular carousel. An example is 51: 3351 is not valid because the second 3 will collide with the 1, even though 51 is a valid 3 diabolo siteswap on its own.
These excited sequences require an additional entrance and exit sequence. You must do 33 4 51515151 41 333 to get in and out of 51. We also write that as 4{51}41 instead of just 51, indicating that the 51 portion can be repeated as many times as desired. Many entrance and exit sequences can be found for each excited siteswap.

Exact height of the numbers

We can not associate a definite height to each number, since it depends on the frequency of the throws. For instance, with 3 diabolos in a high carousel - someone who does a fairly low carousel will do lower 5’s than someone with a higher carousel.

Introduction to passing

Siteswap can also be applied to passing. Numbers for passes are followed by a ‘p’, and sometimes by a number that indicates to which juggler the pass is thrown. In passing there can be passes of non-integer value such as 1.5 or 1.33 (or other fractional values) depending of the time gap between the passes.

The validity process for a sequence becomes slightly more complicated, but the rule of the average stands: (sum of the throws of all the jugglers) / (length of the cycle of the pattern) = the number of diabolos in the pattern.

Some examples of passing patterns on the DVD:
The left part of the sequence is thrown by the first juggler and so on.
< 1.5p 1 | 1 2.5p >: 3 diabolo passing with suns
< 1.5p | 2.5p >: 4 diabolo passing
< 2.5p | 3.5p >: 6 diabolo passing
< 1 1.5p2 | 1.5p1 1.5p3 | 1.5p2 1 >: The feeder (JiBe) feeds on every count.
< 1 2p2 11 | 2p1 1 2p3 1 | 111 2p2 >: The feeder (JiBe) feeds every two counts.

Some examples from the freestyle siteswap clip

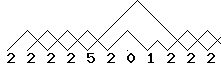5201 (high low pirouette sun): is a sequence that uses 2 diabolos. After a high throw (5), Priam does a small throw (2) which allows him to do a pirouette (0), then a sun (1) before re-throwing the diabolo (2) in order to catch the high throw: 2252012222.

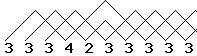42 (high low): THE siteswap trick with 3 diabolos. Instead of throwing 2 diabolos at normal height (33), throw one high (4), followed by one low (2), thus swapping the order of the two diabolos in the carousel.

441 (high high sun): in a low carousel, the 1 is only a break with Baptiste’s 3rd diabolo on the string while the other 2 are in the air. In a high carousel, JiBe does a continuous 441 with a sun between the arms for each 1.

45501 (high high high whip-sun): Priam uses the time offered by the 0 to prepare a two hands whip catch, which he follows with a sun.

50802261 (high throw then low carousel with 2): This sequence combines a 3 high carousel with some 2’s on the string, which calls for a low-notation. The sequence with all preceding and following throws is 6060 50802261 6060. After a slightly lower throw (5) and a higher throw (8 = 4 in high-notation), JiBe has enough time to do two throws of 2 diabolos on the string (22) before resuming the 3 high carousel (616060).

The final word

You can let your imagination go in order to find hundreds of sequences, dozens of ways to use the 0, 00, 000, 1, 11, 111… (all tricks with 0 or 1 diabolo) or to use different techniques for throwing the 2, 3, 4… (behind the back, under the leg, the arms, bounces, grinds, etc…). Running these sequences continuously is another challenge, and can be done in different ways also.
For instance 424242 (Tony) is very different from 42334233 (JiBe).As far as passing is concerned, very little has been done. This is a branch of diabolo that is very rich in variants yet remains largely unexplored. Most regular 2 hand siteswaps associated with balls or clubs can be done in diabolo passing, and numerous variants can be found.